Cladística En Línea
Páginas
Todos pueden colaborar. Para activar su registro por favor envie su email al Editor del blog.
Colaborador(a) registrad@? ... Publique su colaboración aqui>>>
Colaboraciones Recientes
miércoles, 26 de octubre de 2011
Consistencia
El grado de credibilidad de las hipótesis puede evaluarse si se disciernen las fuentes de incertidumbre o desconfianza. Por ejemplo, los tipos de “errores locales” que cuestionan la credibilidad de los datos debido a descripciones o mediciones equivocadas de los caracteres y estados (Patterson & Johnson, 1997) tienen un impacto diferente que el de los “errores de estimación” asociados a los métodos de la reconstrucción filogenética. Los primeros pueden detectarse y corregirse en el laboratorio mismo y tienen impacto sólo en el estudio en cuestión. Pero los del segundo tipo, implican consecuencias metodológicas y conceptuales profundas.
La idea de “consistencia” es que si un método esta libre de errores de estimación, este converge hacia el resultado “correcto” respecto a un marco de referencia, sobre todo cuando los datos son abundantes. En la teoría estadística, un estimador es “consistente” respecto a un modelo especifico cuando su distribución de probabilidad muestra una dispersión menor alrededor del valor “verdadero” conforme el tamaño de la muestra se incrementa. En la teoría filogenética, un método es “consistente” si las hipótesis que produce bajo las condiciones de un modelo particular convergen hacia una filogenia de referencia (Hillis, 1995). Con este propósito, se ha intentado comparar el desempeño de los métodos de parsimonia y los probabilísticos en su habilidad de reconstruir la filogenia. Cuando se evalúa la habilidad de una balanza para estimar el peso correcto, el marco de referencia es el kilo “Patrón” y la variación permitida por una “Norma”. El problema es evidente en el caso de la estimación de la “dispersión” alrededor de la filogenia “correcta” pues los únicos marcos de referencia posibles son los escenarios evolutivos elaborados mediante simulaciones.
Uno de los primeros exámenes de la habilidad de los métodos se basó en una peculiar combinación de datos y modelos (“long branch atraction”) con lo que supuestamente se demostró que parsimonia es “inconsistente”, pues el método no recuperó la topología generada por los datos (Felsenstein, 1978; Kim, 1996). En contraposición, diferentes condiciones simuladas sugirieron que los métodos de verosimilitud también pueden ser “inconsistentes” en su desempeño al estimar la filogenia (Chang, 1996; Farris, 1999; Kolaczkowski & Thornton, 2004; Siddall, 1998). Los intentos de la calificación de métodos en estudios más elaborados solo han llegado a la conclusión de que diseñar simulaciones para medir “consistencia” es un problema muy complejo en el que interactúan tipos de tasas de cambio de los caracteres, tipos de modelos simples o complejos y tipos de topologías simétricas o asimétricas (Goloboff, 2003, Yang, 1996, 1997). Otros, han sugerido que los métodos de parsimonia bajo ciertos modelos son equivalentes a los de verosimilitud (de Queiroz & Poe, 2001, 2003; Steel & Penny, 2000; Tuffey & Steel, 1997).
Parsimonia vs probabilidad
Parsimonia o probabilidad.
El dilema inferencial del taxónomo es cómo saber si una observación de similitud particular (morfológica o molecular), es indicadora de homología filogenética o no lo es (Kluge, 1999). Es decir, la pregunta difícil es: ¿Cuál método es mejor para la reconstruccion de hipótesis de filogenia? Una presuposición básica ante este dilema es que el investigador dispone de dos opciones metodológicas: los métodos basados en parsimonia o los enfoques probabilísticos. La tendencia reciente señala que el uso de los métodos de verosimilitud y Bayesianos va en aumento, a juzgar por el número de usuarios y el de artículos publicados. En la comparación de los atributos de cada método, los respectivos promotores han intentado persuadir que uno u otro enfoque es mejor bajo distintas condiciones empíricas y metodológicas. Por un lado, los argumentos comunmente aluden al desempeño o “consistencia” de los métodos al recuperar filogenias “conocidas” bajo varias situaciones simuladas (Chang, 1996; Farris, 1999; Felsenstein, 1978; Kim, 1996; Kolaczkowski & Thornton, 2004). Por otro lado, las justificaciones o descalificaciones también recurren al uso de las tesis filosóficas de “falsabilidad” y “verificacionismo” en las cuales los métodos de parsimonia o los de verosimillitud se asocian a estas dos posiciones epistemológicas en competencia.
Epistemología de los métodos de reconstrucción.
Una primera linea de razonamiento se basa en la premisa de que los métodos de parsimonia y los probabilísticos representan dos enfoques filosóficos distintos (Siddall & Kluge, 1997; Kluge, 2001b; Doyle & Davis, 1998). Una diferencia entre estos dos enfoques consiste en cómo se concibe filosóficamente el problema de la inferencia de un evento único como la filogenia. Los métodos de parsimonia, bajo un enfoque Popperiano de “falsabilidad”, implicarían que la reconstrucción de historia es un problema de análisis hipotético-deductivo para la identificación de hipótesis de homología (Kluge, 2001b). Epistemológicamente, los métodos cladísticos basados en modelos de parsimonia consisten de varias operaciones lógicas deductivas para proponer hipótesis discretas sobre homología filogenética y cambio de estados a posteriori según el criterio de congruencia máxima. El cladograma más parsimonioso es la mejor explicación lógica implícita en la colección de caracteres (Farris, 1983; Kluge, 2001a).
En contraste, los métodos probabilísticos, bajo un enfoque de “verificabilidad”, presuponen que la inferencia filogenética es un problema inductivo de estimación estadística (Felsenstein, 1982; Yang et al., 1995; Posada, 2003). Los métodos de máxima verosimilitud calculan la probabilidad de los datos (por ejemplo, estados compartidos entre taxa) condicionados a un árbol específico, un modelo seleccionado a priori, una tasa de cambio calculada iterativamente y a un juego de estados ancestrales reconstruidos. Esto no significa que se calcule la probabilidad de que los estados compartidos sean homologos entre taxa. De hecho, mientras que parsimonia depende de hipótesis primarias de homologia, ML es independiente de tales hipótesis (Doyle & Davis, 1998). Cada carácter incrementa la probabilidad asociada a un árbol, pero no en función del concepto de homología sino en relación a un modelo que conjetura la probabilidad de cam-bio en las ramas entre el ancestro y los descendientes. El árbol de la máxima verosimilitud es el mejor resumen enumerativo de la contribución de cada similitud particular.
El intento de la calificación de los métodos de parsimonia o probabilísticos examinando los fundamentos epistemológicos es un ejercicio complejo pero recomendable. Comprensiblemente bajo la premisa de que existe una dicotomia entre la epistemología Popperiana y la perspectiva estadística, todavía prevalece una controversia activa en cuanto a cuál de estas dos posiciones epistemológicas es la más robusta para la reconstrucción filogenética (Carpenter, 1992; Cracraft & Helm-Bychowski, 1991; Felsenstein, 1988, 2001; Felsenstein & Sober, 1986; Goloboff, 2003; Harper, 1979; Kluge, 1997, 2002; Sanderson & Kim, 2000; Steel & Penny, 2000; Trueman, 1993). Presumiblemente dejando las diferencias filosóficas a un lado, los enfoques eclécticos son los más frecuentes bajo la sugestión de que la convergencia de resultados con parsimonia, máxima verosimilitud y probabilidades posteriores Bayesianas es una indicación de la estabilidad de las hipótesis (Cunningham, 1997; Flores-Villela et al., 2000; Giribet, 2003).
Exploración y selección de árboles
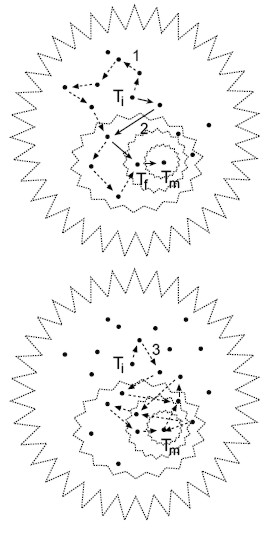
Los primeros esfuerzos de exploración bajo modelos de parsimonia se basaron en la derivación de cadenas heurísticas a partir de muchos árboles iniciales elegidos al azar (Fig. 6). En cada réplica se explora un “sector” (o “isla”) del espacio a partir de un árbol inicial (Ti, Fig. 6) y se visita una cadena de árboles vecinos a los que se llega mediante diferentes algoritmos para el intercambio de ramas (nni, spr, tbr, sensu Kitching et al., 1998, p 45-48). Una cadena de árboles se detiene en el óptimo local cuando ya no se disminuye la longitud de los árboles. Tradicionalmente, para maximizar la posibilidad de encontrar el óptimo global, se replica el esfuerzo de exploración de varios sectores generando cientos de cadenas a partir de igual número de puntos al azar en el espacio. Los programas disponibles (PAUP, Hennig86, NONA, TNT, etc.) permiten evaluar muchas réplicas. Cuando el número de taxa es mayor a 40 o 50, la primera réplica puede tomar demasiado tiempo de computo. En este caso, se idearon maneras de cómo limitar el esfuerzo local en la primera cadena de árboles para favorecer el esfuerzo de exploración global mediante varias réplicas concatenadas (Soltis & Soltis, 1996).
| ||
Figura 6. Exploración del espacio de los árboles. El perfil de valores de todos los árboles para muchos OTU’s configura una superficie análoga a una campana. Aqui se visualizan dos campanas en proyección azimutal. En cada una, los polígonos punteados representan isocontornos de los valores de parsimonia, verosimilitud o probabilidades posteriores. Los puntos son árboles y Ti es un árbol inicial desde el cual parten las rutas heurísticas indicadas por las flechas hasta “subir” al árbol óptimo Tm en la cúspide de la campana. Todas las flechas representan los saltos de un árbol a otro. La cadena 1 ilustra la colección de árboles visitados mediante algún algoritmo de intercambio de ramas y termina en un árbol Tf subóptimo, mientras que la ruta 2 indica la colección de árboles examinados con la estrategia “ratchet” llegando al árbol óptimo. La ruta 3 representa la estrategia azarosa de muestreo de árboles mediante las Cadenas de Markov Monte Carlo. |
Las estrategias de exploración del espacio de árboles desarrolladas durante los últimos diez años han aumentado la velocidad y eficiencia para encontrar árboles óptimos (Goloboff, 1999). La estrategia de exploración ¨matraca¨ (“ratchet”) aumentó la eficiencia de búsqueda debido a ¨brincos¨ azarosos más distantes entre árbol y árbol que los logrados sólo con los algo-ritmos de intercambio de ramas (Nixon, 1999; Vos, 2003). Mediante una matriz de pesos al azar aplicada intermitentemente en cada iteración se modifica drásticamente el rumbo de las cadenas heurísticas, lo cual incrementa la velocidad de exploración de árboles de sectores distintos y la probabilidad de seleccionar árboles óptimos (Fig. 6). Esta estrategia fue denominada “parsimony ratchet”, aunque realmente no es un método de parsimonia; más bien es un algoritmo de búsqueda que puede ser implementado en cualquier método incluyendo los probabilísticos (Vos, 2003). Una estrategia de exploración del universo de árboles aun más eficiente se basa en algoritmos que modelan rutas azarosas de cadenas tipo Markov para combinar valores probables de los parámetros asociados a árboles distintos (MCMC, Huelsenbeck & Ronquist, 2001; SSA, Salter & Pearl, 2001). Los brincos azarosos entre árboles eliminan el esfuerzo de cómputo para el intercambio de ramas o la optimización de la matriz de pesos al azar para decidir cuales árboles se recolectan (Fig. 6). El conjunto de árboles visitados mediante varias cadenas de Markov simultáneas se miden en una fase final de optimización y filtrado (“burn-in”) para seleccionar el conjunto de los óptimos. En cualquiera de las estrategias de búsqueda, sean cadenas concatenadas, “ratchet”, o cadenas de Markov, el criterio de selección del árbol óptimo puede depender de parsimonia, la máxima verosimilitud o probabilidades Bayesianas (Fig. 5).
Métodos de reconstrucción filogenética: Parsimonia
El criterio de parsimonia permite el examen lógico de la congruencia entre cada columna de la matriz de datos y revela la colección máxima de hipótesis de homología táxica y transformacional (De Luna, 1996; Farris, 1983; Kitching et al., 1998). La interacción lógica de varias similitudes particulares (columnas en la matriz de datos) congruentes entre si, selecciona el conjunto de hipótesis de homología putativas y distingue las similitudes homoplásicas (Kluge, 1999). La hipótesis de relaciones filogenéticas asociada al mayor conjunto lógico de homologías contiene a su vez el menor número de homoplasias.
Cuando se contabilizan el total de cambios (homologías y homoplasias) en cada topología según el orden de estados especificadas por un modelo, se obtiene el número de pasos como estimación de su longitud total. El modelo más común es el de Fitch que valora “un paso” al cambio entre cualquier estado (por ejemplo, 0--->1, 0--->2). Otros modelos de parsimonia miden los tipos de cambios entre estados con valores diferentes (Kitching et al., 1998). Bajo cualquier modelo, la topología que implica el menor número de pasos es por tanto la que se selecciona como la óptima. Por ejemplo, para el caso de los tres árboles posibles para cuatro unidades a relacionar (ABCD, Fig. 1), las longitudes serán diferentes cuando se contabilicen los caracteres de una matriz de datos y lógicamente alguna de las topologías será la mínima. Para colecciones grandes de árboles, la frecuencia de los distintos valores de longitud sigue un patrón de distribución semejante al esperado por el modelo Normal. La forma de la campana comunmente no es simétrica, debido a que los datos no se distribuyen azarosa-mente entre los taxa. Sea que los datos exhiben un nivel alto de congruencia o de incongruencia las distribuciones tienden a estar sesgadas hacia la izquierda o hacia la derecha (Hillis, 1991; Hillis & Huelsenbeck, 1992).
Parsimonia es un criterio extra-evidencial para seleccionar la mejor hipótesis entre varias igualmente soportadas por los datos. La evidencia tiene un papel limitado cuando los mismos datos apoyan varias hipótesis alternativas. En esta situación se puede hacer uso del autoritarismo, convencionalismo o parsimonia como criterios de selección de inferencias (ver revisión por De Luna, 1996). Ante varias hipótesis igualmente apoyadas por los datos, el uso de parsimonia selecciona la que satisface dos propiedades lógicas: “causa común” y “sencillez”. El principio de “causa común” favorece hipótesis que explican los mismos efectos, en relación a la misma causa. El uso de parsimonia en la ciencia en general presupone que para los mismos efectos naturales, podemos hipotetizar las mismas causas (Reichenbach, 1956; Salmon, 1984). Por ejemplo, en sistemática inferir “ancestría común” es un caso de la aplicación del principio de causa común (Sober, 1988). Complementariamente, el uso de parsimonia como principio de “sencillez” favorece las hipótesis científicas que son sencillas como descripción o explicación. Entre varias hipótesis igualmente lógicas y empíricamente consistentes, se elige la explicación más sencilla, es decir, la que explica el dominio con el menor número de conjeturas. Así es como una recta (a, Fig. 2) se prefiere por su sencillez algebraica comparada con otras hipótesis (b, c, Fig. 2) al explicar cualquier fenómeno por más complejo que sea. El uso de parsimonia por lo tanto implica sencillez en la descripción del dominio, no presupone simplicidad como propiedad del dominio descrito o explicado (Farris, 1983; Kluge, 1984). El dominio puede ser sencillo o muy complejo (Crisci, 1982), lo cual es irrelevante en la selección de hipótesis en competencia para describir tal dominio. Por ejemplo, las hipótesis de filogenia son parsimoniosas en el sentido de la descripción o explicación del dominio, pero el proceso evolutivo como dominio explicado puede ser muy complejo.
El procedimiento de cálculo del árbol más parsimonioso es no-paramétrico y consiste en construir la red más corta que conecta todas las unidades de muestreo (OTU’s) en el espacio Euclidiano multidimensional. Los árboles de parsimonia se conciben como un caso particular de las redes de Steiner que unen puntos en un espacio multidimensional configurado por los caracteres como ejes (Semple & Steel, 2003, p. 97). Los OTU’s son puntos o vectores L con diferentes posiciones en este espacio, (Fig. 3). Las coordenadas de la ubicación de un vector L(c1, …, cr) están dadas por los valores observados en cada carácter (c). La dimensión del espacio (r=c) es infinita pues crece cada vez que se agregan más caracteres. Se han propuesto varios modelos no-paramétricos de distancias para medir la longitud de las redes, por ejemplo, distancias Euclidianas, de Manhattan, de Nei, etc. También se han formulado varios modelos noparamétricos de parsimonia, por ejemplo, Wagner, Fitch, etc. para medir las redes en términos de “pasos” o eventos evolutivos. Los métodos cladísticos basados en modelos de parsimonia estiman la distancia patrística calculando la suma del número de cambios de estado (pasos) en cada rama.
Modelos
Una vez recolectado un conjunto de caracteres, el siguiente paso es la selección de un modelo que postule el valor de los cambios entre estados. Varios modelos ya formulados incorporan distintas suposiciones sobre el valor de los tipos de transformaciones (Schultz et al., 1996; Swofford & Maddison, 1987; Posada, 2003; Posada & Crandall, 2001). Nuestro papel en la gran mayoría de los casos no es formularlos, sino especificarlos y luego validarlos adecuadamente mediante cálculos de algún tipo de “ajuste” del modelo a los datos. Los dos tipos de modelos disponibles para medir topologías y seleccionar árboles óptimos son los de parsimonia (Wagner, Fitch, Dollo, Camin-Sokal, etc, Kitching et al., 1998) y los probabilísticos (Jukes-Cantor, Kimura 2P, etc., Posada & Crandall, 2001).
Los de parsimonia valoran los cambios entre estados en unidades de “pasos” o eventos evolutivos y dependen del concepto de homología filogenética y los métodos para establecer orden de estados (Mabee, 1989). Un carácter con tres estados (0, 1, 2) implica dos eventos entre 0 y 2 según los valores especificados en el modelo de Wagner, pero sólo vale un “paso” en el modelo de Fitch. La “dispersión” del modelo se mide en términos del número de pasos o eventos de cambio extra que implica un árbol particular. Bajo este enfoque, el árbol más corto es el que mejor “ajusta” los datos (Farris, 1983; Sober, 1988).
Figura 2. La interacción de los modelos, los datos y los árboles en los métodos de reconstrucción filogenética. Los modelos se aplican a los datos para explicar su dispersión y se validan al medir el ajuste. En las gráficas de la izquierda, la recta “a” es más parsimoniosa que las otras dos curvas (b y c), pero a1, a2 y a3 son igualmente parsimoniosas. Del mismo modo, el árbol más parsimonioso y el de la máxima verosimilitud se interpretan como los que maximizan el ajuste. Al considerar las dos topologías (((A,B)C) (D,E)), la medida de parsimonia es idéntica. No obstante, una de estas dos topologías sería juzgada “mejor” si se estima bajo métodos de máxima verosimilitud. Dependiendo del modelo, la medida de verosimilitud es diferente para la misma topología debido a los distintos valores de las longitudes de las ramas (L1, L2, L3, L4).
Los modelos probabilísticos se basan en el concepto estadístico de verosimilitud como la probabilidad de observar la colección de datos si un árbol específico fuera el verdadero (Felsenstein, 1981; Lewis, 1998). La “dispersion” se mide en función del acuerdo o ajuste entre los datos observados y las predicciones calculadas por un árbol particular y un modelo. Bajo este enfoque, el árbol óptimo es el de la máxima verosimilitud (Steel & Penny, 2000) o el de la probabilidad posterior Bayesiana más alta (Rannala & Yang, 1996).
Los métodos para la selección del mejor modelo de cambio entre estados difieren bajo los enfoques de parsimonia o probabilisticos. Bajo el primero, no hay necesidad a priori de evaluar por ejemplo si Fitch es mejor que Wagner al interpretar el orden de estados. Los caracteres multiestado se hipotetizan “sin orden” o se codifican binariamente. Los métodos para derivar las hipótesis de cambio de estados (ACCTRAN, DELTRAN, etc) son a posteriori en función de las transformaciones implícitas en el árbol óptimo escogido (Grant & Kluge, 2004; Kornet & Turner, 1999). En contraste, en los enfoques probabilísticos los modelos de cambio son un prerequisito para iniciar la reconstrucción filogenética. La selección de la mejor hipótesis de cambio de estados es a priori, aunque además de los datos, esta estimación también depende de un árbol de referencia. Comúnmente se calcula una medida de similitud total derivada de los datos y un algoritmo de “agrupamiento de vecino más cercano” (neighbour joining) produce el árbol requerido. Estos procedimientos se han implementado en programas como ModelTest para identificar el mejor modelo de cambio según la correspondencia de los datos y el árbol de referencia (Posada, 2003; Posada & Crandall, 2001; Yang, 1997). El modelo preferido se aplica entonces para iniciar la búsqueda del árbol óptimo en programas como “PAUP” o “MrBayes”, los cuales miden la verosimilitud o las probabilidades Bayesianas de los árboles en competencia.
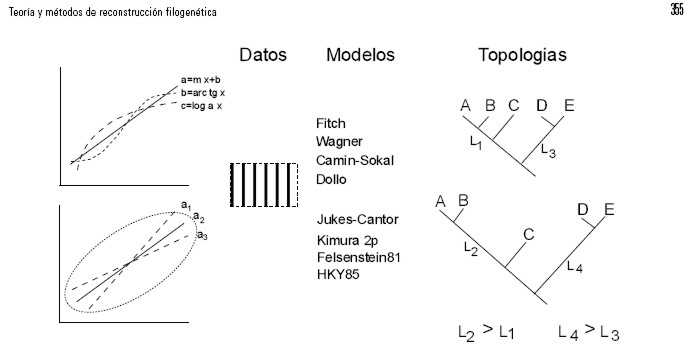
Figura 2. La interacción de los modelos, los datos y los árboles en los métodos de reconstrucción filogenética. Los modelos se aplican a los datos para explicar su dispersión y se validan al medir el ajuste. En las gráficas de la izquierda, la recta “a” es más parsimoniosa que las otras dos curvas (b y c), pero a1, a2 y a3 son igualmente parsimoniosas. Del mismo modo, el árbol más parsimonioso y el de la máxima verosimilitud se interpretan como los que maximizan el ajuste. Al considerar las dos topologías (((A,B)C) (D,E)), la medida de parsimonia es idéntica. No obstante, una de estas dos topologías sería juzgada “mejor” si se estima bajo métodos de máxima verosimilitud. Dependiendo del modelo, la medida de verosimilitud es diferente para la misma topología debido a los distintos valores de las longitudes de las ramas (L1, L2, L3, L4).