Exploración y selección de árboles

Exploración del espacio y selección de árboles óptimos. Entre los avances teóricos y metodológicos más notables destacan las estrategias dirigidas para la estimación y la selección de topologías óptimas. Uno de los problemas de estimación filogenética es que, independientemente de la existencia de datos y los modelos de cambio, para cada colección de unidades de estudio (OTU’s) existe un conjunto muy grande, aunque limitado, de todos los árboles posibles topológicamente distintos que relacionan esos taxa. Por ejemplo para 5 taxa el conjunto consiste de 15 topologías no enraizadas diferentes (Fig. 1, 5); para 20 unidades, el número de topologías es mayor a 2.21x1020 (221 643 095 476 699 771 875 ¡exactamente!). En estas condiciones, todos los métodos para calcular el mejor árbol (parsimonia o probabilísticos) usan algoritmos de exploración aproximados (heurísticos). La operación básica consiste en sondear “sectores” del espacio escogiendo árboles como puntos de inicio y visitando árboles vecinos o intentando saltos a otros árboles en “sectores” distantes. El objetivo es medir los valores de optimización de una muestra de árboles en función de una matriz de datos y seleccionar el mejor. Los resultados varían de intento en intento, por lo que la búsqueda heurística se replica muchas veces hasta que el valor óptimo de parsimonia, verosimilitud o probabilidad posterior se estabiliza.

Los primeros esfuerzos de exploración bajo modelos de parsimonia se basaron en la derivación de cadenas heurísticas a partir de muchos árboles iniciales elegidos al azar (Fig. 6). En cada réplica se explora un “sector” (o “isla”) del espacio a partir de un árbol inicial (Ti, Fig. 6) y se visita una cadena de árboles vecinos a los que se llega mediante diferentes algoritmos para el intercambio de ramas (nni, spr, tbr, sensu Kitching et al., 1998, p 45-48). Una cadena de árboles se detiene en el óptimo local cuando ya no se disminuye la longitud de los árboles. Tradicionalmente, para maximizar la posibilidad de encontrar el óptimo global, se replica el esfuerzo de exploración de varios sectores generando cientos de cadenas a partir de igual número de puntos al azar en el espacio. Los programas disponibles (PAUP, Hennig86, NONA, TNT, etc.) permiten evaluar muchas réplicas. Cuando el número de taxa es mayor a 40 o 50, la primera réplica puede tomar demasiado tiempo de computo. En este caso, se idearon maneras de cómo limitar el esfuerzo local en la primera cadena de árboles para favorecer el esfuerzo de exploración global mediante varias réplicas concatenadas (Soltis & Soltis, 1996).

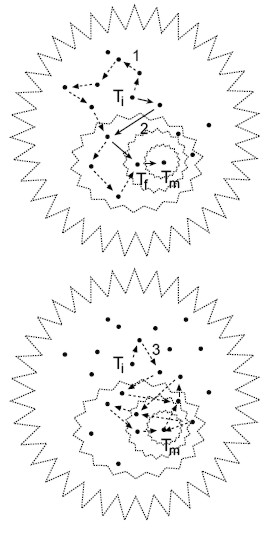
	Figura 6. Exploración del espacio de los árboles. El perfil de valores de todos los árboles para muchos OTU’s configura una superficie análoga a una campana. Aqui se visualizan dos campanas en proyección azimutal. En cada una, los polígonos punteados representan isocontornos de los valores de parsimonia, verosimilitud o probabilidades posteriores. Los puntos son árboles y Ti es un árbol inicial desde el cual parten las rutas heurísticas indicadas por las flechas hasta “subir” al árbol óptimo Tm en la cúspide de la campana. Todas las flechas representan los saltos de un árbol a otro. La cadena 1 ilustra la colección de árboles visitados mediante algún algoritmo de intercambio de ramas y termina en un árbol Tf subóptimo, mientras que la ruta 2 indica la colección de árboles examinados con la estrategia “ratchet” llegando al árbol óptimo. La ruta 3 representa la estrategia azarosa de muestreo de árboles mediante las Cadenas de Markov Monte Carlo.

Las estrategias de exploración del espacio de árboles desarrolladas durante los últimos diez años han aumentado la velocidad y eficiencia para encontrar árboles óptimos (Goloboff, 1999). La estrategia de exploración ¨matraca¨ (“ratchet”) aumentó la eficiencia de búsqueda debido a ¨brincos¨ azarosos más distantes entre árbol y árbol que los logrados sólo con los algo-ritmos de intercambio de ramas (Nixon, 1999; Vos, 2003). Mediante una matriz de pesos al azar aplicada intermitentemente en cada iteración se modifica drásticamente el rumbo de las cadenas heurísticas, lo cual incrementa la velocidad de exploración de árboles de sectores distintos y la probabilidad de seleccionar árboles óptimos (Fig. 6). Esta estrategia fue denominada “parsimony ratchet”, aunque realmente no es un método de parsimonia; más bien es un algoritmo de búsqueda que puede ser implementado en cualquier método incluyendo los probabilísticos (Vos, 2003). Una estrategia de exploración del universo de árboles aun más eficiente se basa en algoritmos que modelan rutas azarosas de cadenas tipo Markov para combinar valores probables de los parámetros asociados a árboles distintos (MCMC, Huelsenbeck & Ronquist, 2001; SSA, Salter & Pearl, 2001). Los brincos azarosos entre árboles eliminan el esfuerzo de cómputo para el intercambio de ramas o la optimización de la matriz de pesos al azar para decidir cuales árboles se recolectan (Fig. 6). El conjunto de árboles visitados mediante varias cadenas de Markov simultáneas se miden en una fase final de optimización y filtrado (“burn-in”) para seleccionar el conjunto de los óptimos. En cualquiera de las estrategias de búsqueda, sean cadenas concatenadas, “ratchet”, o cadenas de Markov, el criterio de selección del árbol óptimo puede depender de parsimonia, la máxima verosimilitud o probabilidades Bayesianas (Fig. 5).