Modelos

Cualquiera que sea la naturaleza de los datos, morfológicos o moleculares, las observaciones por sí solas no seleccionan directamente una topología, sino que debe aplicarse algún modelo de cambio entre estados para elegir entre las hipótesis (topologías) alternativas (Farris, 1983; Sober, 1988; Steel & Penny, 2000; Posada, 2003). La interacción epistemológica entre datos, modelos e hipótesis en sistemática puede ilustrarse con el caso estadístico de seleccionar la mejor función de ajuste entre tres alternativas (Fig. 2). Cada línea representa un modelo disponible (logarítmico, recta, etc.) entre los cuales se ha de escoger uno para explicar los datos recolectados. El modelo seleccionado se aplica para estimar los mejores parámetros calculados para minimizar la dispersión de los datos. Por ejemplo, si se decide aplicar algún modelo lineal (regresión simple, eje principal, eje mayor reducido), la estimación de los parámetros consiste en seleccionar la mejor pendiente de la recta que minimiza la varianza de Y o la covarianza de XY, dependiendo del modelo. Del mismo modo, en la reconstrucción filogenética primero especificamos las suposiciones de cambio entre estados en un modelo y luego lo aplicamos para estimar la mejor topología que explica la distribución de los caracteres entre las unidades de estudio, es decir, proponemos la mejor topología bajo ese modelo (Page & Holmes, 1998).

Una vez recolectado un conjunto de caracteres, el siguiente paso es la selección de un modelo que postule el valor de los cambios entre estados. Varios modelos ya formulados incorporan distintas suposiciones sobre el valor de los tipos de transformaciones (Schultz et al., 1996; Swofford & Maddison, 1987; Posada, 2003; Posada & Crandall, 2001). Nuestro papel en la gran mayoría de los casos no es formularlos, sino especificarlos y luego validarlos adecuadamente mediante cálculos de algún tipo de “ajuste” del modelo a los datos. Los dos tipos de modelos disponibles para medir topologías y seleccionar árboles óptimos son los de parsimonia (Wagner, Fitch, Dollo, Camin-Sokal, etc, Kitching et al., 1998) y los probabilísticos (Jukes-Cantor, Kimura 2P, etc., Posada & Crandall, 2001).

Los de parsimonia valoran los cambios entre estados en unidades de “pasos” o eventos evolutivos y dependen del concepto de homología filogenética y los métodos para establecer orden de estados (Mabee, 1989). Un carácter con tres estados (0, 1, 2) implica dos eventos entre 0 y 2 según los valores especificados en el modelo de Wagner, pero sólo vale un “paso” en el modelo de Fitch. La “dispersión” del modelo se mide en términos del número de pasos o eventos de cambio extra que implica un árbol particular. Bajo este enfoque, el árbol más corto es el que mejor “ajusta” los datos (Farris, 1983; Sober, 1988).

Figura 2. La interacción de los modelos, los datos y los árboles en los métodos de reconstrucción filogenética. Los modelos se aplican a los datos para explicar su dispersión y se validan al medir el ajuste. En las gráficas de la izquierda, la recta “a” es más parsimoniosa que las otras dos curvas (b y c), pero a1, a2 y a3 son igualmente parsimoniosas. Del mismo modo, el árbol más parsimonioso y el de la máxima verosimilitud se interpretan como los que maximizan el ajuste. Al considerar las dos topologías (((A,B)C) (D,E)), la medida de parsimonia es idéntica. No obstante, una de estas dos topologías sería juzgada “mejor” si se estima bajo métodos de máxima verosimilitud. Dependiendo del modelo, la medida de verosimilitud es diferente para la misma topología debido a los distintos valores de las longitudes de las ramas (L1, L2, L3, L4).

Los modelos probabilísticos se basan en el concepto estadístico de verosimilitud como la probabilidad de observar la colección de datos si un árbol específico fuera el verdadero (Felsenstein, 1981; Lewis, 1998). La “dispersion” se mide en función del acuerdo o ajuste entre los datos observados y las predicciones calculadas por un árbol particular y un modelo. Bajo este enfoque, el árbol óptimo es el de la máxima verosimilitud (Steel & Penny, 2000) o el de la probabilidad posterior Bayesiana más alta (Rannala & Yang, 1996).

Los métodos para la selección del mejor modelo de cambio entre estados difieren bajo los enfoques de parsimonia o probabilisticos. Bajo el primero, no hay necesidad a priori de evaluar por ejemplo si Fitch es mejor que Wagner al interpretar el orden de estados. Los caracteres multiestado se hipotetizan “sin orden” o se codifican binariamente. Los métodos para derivar las hipótesis de cambio de estados (ACCTRAN, DELTRAN, etc) son a posteriori en función de las transformaciones implícitas en el árbol óptimo escogido (Grant & Kluge, 2004; Kornet & Turner, 1999). En contraste, en los enfoques probabilísticos los modelos de cambio son un prerequisito para iniciar la reconstrucción filogenética. La selección de la mejor hipótesis de cambio de estados es a priori, aunque además de los datos, esta estimación también depende de un árbol de referencia. Comúnmente se calcula una medida de similitud total derivada de los datos y un algoritmo de “agrupamiento de vecino más cercano” (neighbour joining) produce el árbol requerido. Estos procedimientos se han implementado en programas como ModelTest para identificar el mejor modelo de cambio según la correspondencia de los datos y el árbol de referencia (Posada, 2003; Posada & Crandall, 2001; Yang, 1997). El modelo preferido se aplica entonces para iniciar la búsqueda del árbol óptimo en programas como “PAUP” o “MrBayes”, los cuales miden la verosimilitud o las probabilidades Bayesianas de los árboles en competencia.

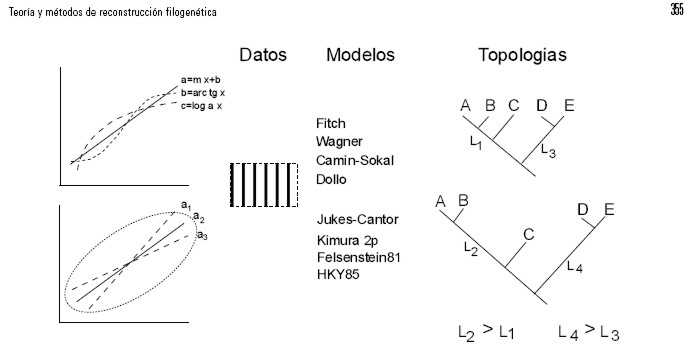
Figura 2. La interacción de los modelos, los datos y los árboles en los métodos de reconstrucción filogenética. Los modelos se aplican a los datos para explicar su dispersión y se validan al medir el ajuste. En las gráficas de la izquierda, la recta “a” es más parsimoniosa que las otras dos curvas (b y c), pero a1, a2 y a3 son igualmente parsimoniosas. Del mismo modo, el árbol más parsimonioso y el de la máxima verosimilitud se interpretan como los que maximizan el ajuste. Al considerar las dos topologías (((A,B)C) (D,E)), la medida de parsimonia es idéntica. No obstante, una de estas dos topologías sería juzgada “mejor” si se estima bajo métodos de máxima verosimilitud. Dependiendo del modelo, la medida de verosimilitud es diferente para la misma topología debido a los distintos valores de las longitudes de las ramas (L1, L2, L3, L4).